ブンセキマラソンその１　「要約統計量・度数集計・ヒストグラム」

始まりましたブンセキマラソン(仮)初回は要約統計量・度数集計・ヒストグラムの３点盛り！

説明のためにまずはヒストグラムから解説します。

ヒストグラム

f:id:fujit33:20151003214102j:plain
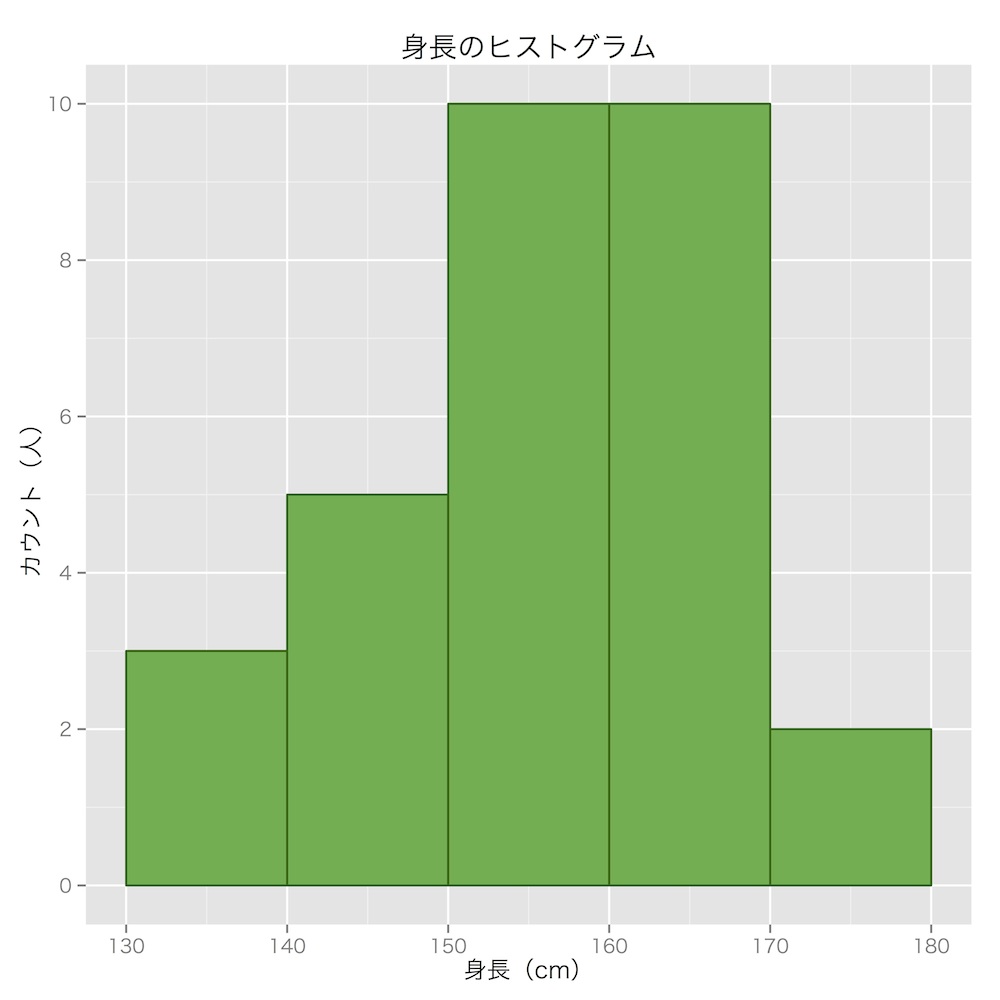
ヒストグラムとはこのような棒グラフっぽいものでデータの分布を視覚的に捉えるものです。でも棒グラフと違うのは、値を区切ってまとめていること！
たとえば、このヒストグラムでは130と140の間に3人居ることを表しています。ここでは「130cm台」としてまとめてしまっていますが、本当は133,136,139というデータが中にあります。このように、データをまとめることで全体の傾向が見やすくなっているのがヒストグラム。
ヒストグラムは棒の間に隙間を作らずに描きます。

要約統計量とは

データを要約した値が要約統計量。例を挙げたほうが早い。

平均(mean)

データの合計をデータの個数で割ったもの。とってもよく使う。
${ \displaystyle 平均 \mu = \frac{1}{N}(x_1+x_2+x_3\cdots) = \frac{1}{N}\sum_{i=1}^{N} x_i }$

中央値(median)

得られたデータを小さい順に並べて、ちょうど真ん中の順番になった値。ただし、データが偶数の場合、真ん中の２つの値の平均値。

例：
「0,1,2,3,4,5,6,7,8,9,10」というデータの中央値は「5」

最頻値(mode)

データの中で回数が最も多く現れる値。複数あることもある。

例：
「0,1,2,3,3,3,4,4,5,5,6」というデータの最頻値は「3」

分散・標準偏差

分散・標準偏差はデータの「ばらつき」を示す値。標準偏差は分散の平方根（ルート）なので、それぞれが示す意味は同じ。

分散はデータの値ひとつひとつの「平均との差」を二乗し（マイナスの差もプラスにするため）てすべて合計し、それをデータの個数で割った（データの個数に影響されないため）もの。
式で表すと
${ \displaystyle 分散V = \frac{1}{N}{(x_1-\overline{x})^2+(x_2-\overline{x})^2+(x_3-\overline{x})^2\cdots} = \frac{1}{N}\sum_{i=1}^{N} (x_i-\overline{x})^2 }$
${ \displaystyle 標準偏差σ = \sqrt{V} }$
分散や標準偏差が大きいほど、平均から離れたところにデータが沢山あるということ。

例えば、同じ人たちが３つのテストを受験したらどれも平均は60点だった。しかし、標準誤差が違った場合、このようなヒストグラムになります。
f:id:fujit33:20151005151428j:plain
赤いテストは標準偏差10、緑は15、青は20
標準偏差が小さいほど、データがばらつかず、標準偏差が大きいほどデータがばらけることがよく分かると思います。

平均信じるな！

平均値はとてもわかりやすく便利な値ですが、むやみに平均値を鵜呑みにするとデータを間違って解釈する恐れがあります。実際、世の中のデータは平均値で表せないデータばかりです。
例えば、次のグラフはTwitterにおける、一日あたりの平均ツイート数のヒストグラムです。
f:id:fujit33:20151011202855j:plain
データがかなり左に偏っているが、右にも長く伸びていることがわかります。つまり、ほとんどの人は１日あたりツイート数が少ないが、少数の人々は日々大量にツイートを投稿するヘビーユーザーであるとわかります。このようなデータで中央値と平均値を計算してみるとどうなるでしょうか。
f:id:fujit33:20151011202845j:plain
中央値と平均値にかなり大きな差がでてしまうことが分かります。このように、大きく偏っているデータでは、平均値よりも中央値を用いたほうが良いことがあることを覚えておかなければいけません。（注意点として、このデータは機械的に自動投稿するユーザーも含んでいるので、感覚よりも多くなっています。）